Block diagram of computer, Number system and complements

Chapter 1

Block diagram of a digital computer

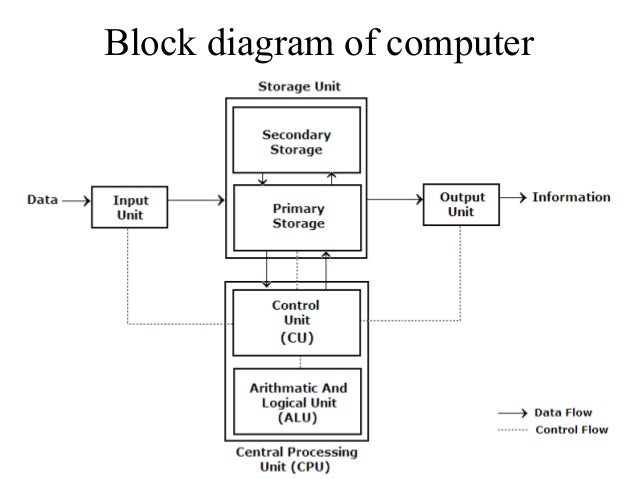
The Hardware of the digital computer is usually divided into these major parts. The CPU contains arithmetic and logic unit for manipulating data, a number of registers for storing data and control a disc. The memory is for storage purpose which is called Random access Memory. The IOP contains electronic circuit for communicating and controlling the transfer of information between computer and outside world.

Advantage of digital system

·         Digital signal can be transmitted without degradation due to noise.

·         More precise representation of a signal can be obtained by increasing the no of bits.

·         Digital signal can be controlled by software allowing new functions to be added without changing hardware.

·         Information storage can be easier in digital system.

Disadvantages

In some system if a single piece of digital data is lost or misinterpreted, the meaning of large block of related data can completely change.

Number systems

1.     Decimal Number System

The decimal number system is said to be one of base (or radix) 10 number system because it uses the 10 different symbols from 0-9, to represent any data.

E.g.:- (7392)₁₀=7*10³+3*10²+9*10¹*2*10⁰

2.     Binary Number System

The binary number system is a radix 2 number system as it contains only two positive digits 0 and1.

E.g. :-( 1011)₂=1*2³+0*2²+1*2¹+1*2⁰=8+2+1= (11)₁₀

3.     Octal Number System

The Octal number system is a radix 8 number system as it contains 8 different symbols from (0-7).

E.g.:- (1274)₈ is an octal data.

4.     Hexadecimal Number System

This number system is a base 16 number system since it contains 16 different symbols to represent a data. It borrows 10 symbols from decimal system and 6 systems from the letter of alphabet (A, B, C, D, E, and F).

E.g.:- (B44B) ₁₆ is a hexadecimal data.

Complements

This is the representation for the negative numbers.

Types

·         r’s complement

·         (r-1)’s complement

(r-1)’s complement

For any given data the (r-1)’s complement of the data is calculated as (rⁿ-1)-N where r is the base of the corresponding number system. N is the number to be complemented, n is the total number of digits. In case of decimal data the value of r is 10 and for binary the value of r is 2. So the (r-1)’s complement and 9’s complement is for binary and decimal number respectively.

Example:

1’s complement of 101101

Here N=101101

         (n)= 6

         (r)=2

So 1’s complement is (rⁿ-1)-N= (2⁶-1)-101101= (1000000-1)-101101= 010010 is the 1’s complement of given number.

9’s complement of 56732

Here N= 56732 (n) = 5 (r) = 10

So (r-1)’s complement= (rⁿ-1)-N= (10⁵-1)-56732= 99999-56732= 43267

r’s complement

The r’s complement of any data having base (r) is calculated using formula (rⁿ-N), where r is base of corresponding number system, n  is the total no of digits and N is the corresponding number so for decimal and binary number systems the r’s complement means 10’s complement and 2’s complement respectively.

Example

r’s complement of following data:

a)      (10010)₂ 

b)      (3297)₁₀

a) (10010)₂

It is a binary data and hence r=2 n=5 N=10010

We know,

     r’s complement= rⁿ-N= 2⁵-10010= 100000-10010= 01110

b) (3297)₁₀

It is a decimal data and hence r=10, N=3297, n=4

We know,

   r’s complement= rⁿ-N= 10⁴-3297= 10000-3297= 6703

Subtractions with complements

Subtractions using r’s complement

The subtractions of two n digit numbers M and N in base r can be done as following:

1.       Add Minuend ‘M’ with the r’s complement of subtrahend N. Mathematically M-N= M+ (rⁿ-N) = M-N+rⁿ.

2.       If M≥N, the sum will produce an end carry, which on discarding gives required answer.

3.       If M<N, the sum doesn’t produce an end carry, which is in the form of r’s complement of (N-M). In this case to represent the number in user friendly form, find the complement of the sum and put a (-) sign in front of it.

Example

Using 10’s complement, subtract 52532-3250.

Here, M=52532 N=03250 (making no of digits in Minuend and subtrahend equal)

10’s complement of subtrahend (N) = 99999-03250+1=96750

Adding it with minuend (M), we get,

53532+96750= (1)49282 here 1 is end carry so on discarding 1 we get 49282 which is the required difference.

Note: Make no of digits in minuend and subtrahend equal if not so

Using 2’s complement, subtract 1010100-1000011.

Here, M=1010100 N=1000011, then 2’scomplement of N Is 0111101.

Adding the 2’s complement of N to the Minuend we get,

1010100+0111101= (1)0010001 here 1 is end carry so on discarding it we get required difference=001001.

Subtractions using (r-1)’s complement

The subtractions of two n digit numbers M and N in base r can be done as following:

1.       Add minuend ‘M’ to the (r-1)’s complement of subtrahend N. Mathematically,                             M-N=M+ (rⁿ-N)-1= M-N+rⁿ-1.

2.       If M≥N, the sum will produce an end carry, which is discarded and 1 is added to it, where 1 is called end around carry.

3.       If M<N, the sum doesn’t produce an end carry, which is in the form of (r-1)’s complement of (N-M). In the case to represent the number in user friendly form, find the (r-1)’s complement of the sum and put a (-) sign in front of it.

Example

Given the two binary numbers, 1010100 and 1000011, perform the subtraction using 1’s complement.

Here,

  Minuend (M) =1010100 subtrahend (N) =1000011. 1’s complement of (N) =0111100

Adding 1’s complement with M, we get,

1010100+0111100= (1)0010000 here 1 is end carry discarding it and then adding end around carry we get, 0010000+1=0010001 which is the required answer.

Subtract 7352-4201 using 9’s complement.

Here Minuend (M) = 7352 and subtrahend (N) = 4201

9’complement of subtrahend (N) = 9999-4201=5798

Adding with Minuend 5798+7352= (1)3150 here 1 is end carry so discarding it and then adding end around carry we get 3150+1=3151 which is the required answer.